Makroekonomická rovnováha v čase

Příklad ze cvičení

Makroekonomická rovnováha v čase

Určete, jak se vyvíjí důchod v čase, je-li mpc = 0,6; autonomní C = 160; autonomní I = 40. Zpoždění mezi důchodem a poptávkou je o jedno období.

• Jaká je statická rovnováha? Také obecně.
• Zapiš rovnici zpožděné AD v jednosektorové ekonomice.
• ... ve dvousektorové.
• Jaký je vývoj důchodu v dlouhém období (řeš diferenční rovnici)?
• Urči vývoj důchodu pro počáteční podmínku důchod v čase nula = 600. 
• Situaci zakresli.
• Zapiš obecně, kam se blíží důchod v dlouhém období (limitou.)

Dynamický model S-D, zpoždění na straně poptávky

• Přehoď v modelu S-D (viz předchozí příklady) zpoždění na stranu poptávky, a to pro oba předchozí poměry sklonů S, resp. D.
• Řeš nejprve matematicky a pak teprve graficky. Zkontroluj pokaždé souhlas.
• Zapiš přehledně a systematicky všechny čtyři případy dynamické rovnováhy S-D pro nespojité změny.

Nekonvergentní nespojitý model S-D při zpoždění na straně nabídky

• Přehoď vzájemný poměr sklonů z předchozích příkladů.
• Vykonej všechny kroky z předchozích příkladů.
• Přehledně zapiš srovnání.

Početní určení konvergence v pavučinovém modelu S-D

• Mějme S: Q = - 1 + 2 P; D: Q = 24 - 3 P; počáteční cena je rovna 3 jednotkám. Zpoždění je o jedno období straně nabídky.
• Zapiš rovnice dynamické rovnováhy, tj. diferenční rovnici.
• Řeš rovnici ve všech bodech s matematickým popisem.
• Spočti také partikulární řešení odpovídající počáteční podmínce.
• Vypiš předpis (funkci), která charakterizuje vývoj cen v čase.
• Interpretuj řešení, tj. vytvoř tabulku hodnot nalezené funkce vývoje cen v čase.
• Zakresli vývoj cen v čase, resp. vývoj odchylek v čase (z hodnot v tabulce).
• Zkontroluj správnost porovnáním s grafickým řešením, resp. s intuitivním odhadem.
• Změň počáteční podmínku na počáteční cenu rovnu 2 jednotkám. Zakresli, popiš.
• Interpretuj, co znamená změna počáteční podmínky (dle grafu). 

Grafické určení a znázornění konvergence v pavučinovém modelu S-D

• Mějme S: Q = - 1 + 2 P; D: Q = 24 - 3 P; počáteční cena je rovna 3 jednotkám. Zpoždění je o jedno období na straně nabídky.
• Zakresli S, D do přehledného grafu přesně v měřítku.
• Vyznač vývoj tlaků na změny ceny v čase, tj. zakresli "pavučinu" ke grafu S-D.
• Vyznač velikost odchylek od rovnovážné ceny na straně nabídky. Označ p0, p1, p2 atd.
• Zakresli graf vývoje odchylek, resp. absolutních hodnot odchylek v čase.
• Zakresli vývoj cen v čase.
• Zapiš limitu týkající se vývoje odchylek v čase a odpovídající konvergenci, resp. divergenci modelu.

Intuitivní odhad konvergence v pavučinovém modelu S-D

• Mějme S: Q = - 1 + 2 P; D: Q = 24 - 3 P; počáteční cena je rovna 3 jednotkám. Zpoždění je o jedno období na straně nabídky.
• Odhadněte intuitivně (pomocí porovnání sklonů S, D), zda je model konvergentní, tj. zda situace spěje k rovnovážné ceně.
• Jedná se o model nespojitý nebo spojitý?

Extrémní účinky fiskální, resp. monetární politiky

• Systemizuj všechny případy extrémní účinnosti fiskální, resp. monetární politiky. 
• Vždy zakresli obrázek, popiš účinnost na základě grafického vyjádření.
• Pro každý případ spočti účinnost na základě limity multiplikátoru.

Změna důchodu vlivem změny nabídky peněz

• Pro výše zadanou ekonomiku zvol změnu nabídky peněz.
• Počítej dvěma metodami (multiplikátory, resp. průsečíky přímek)
• Řeš graficky (přesný nákres se změřením délek úseček).
• Výsledky porovnej. V případě neshody oprav.

Velikost vytěsněné produkce vlivem změny daňové sazby

Urči velikost vytěsněné produkce vlivem snížení daňové sazby z hodnoty 0,25 na hodnotu 0,20.

• Ekonomika je popsána stejně jako v předchozím příkladě.
• Lze počítat oběma metodami jako v předchozím příkladě?
• Řeš také graficky (přesné zakreslení a ověření hodnot z grafu).
• Zapiš výsledky početního i grafického výpočtu symbolicky s využitím implikací (jako pravidlo). Došlo k posunu nebo otočení přímek v modelu IS-LM, a které.

Velikost vytěsněné produkce vlivem změny  vládních výdajů

Urči velikost vytěsněného produktu vlivem fiskální politiky vlády v podobě zvýšení vládních výdajů o 100 jednotek. 

• Počítej pro autonomní spotřebu 100, mpc = 0,8; pro t = 0,25; transfery jsou ve výši 125 a vládní výdaje 400. L = 0,5.Y - 50.i; I = 300 - 30.i; nabídka peněz vztažená k cenové hladině je 500.
• Počítej dvěma metodami, a to (a) srovnáním multiplikátorů a (b) určením průsečíků přímek a jejich souřadnic důchodu. 
• Řeš také graficky (přesné zakreslení a ověření hodnot z grafu).
• Zapiš výsledky početního i grafického výpočtu symbolicky s využitím implikací (jako pravidlo). Došlo k posunu nebo otočení přímek v modelu IS-LM, a které.

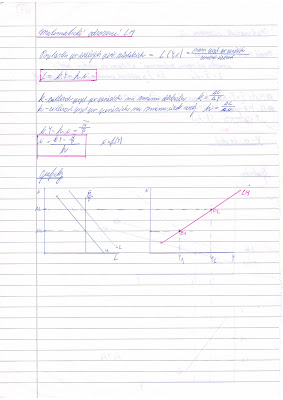
Změna sklonu LM vlivem změny k, resp. h

  Změna k

• Analyzuj početně i graficky pro k = 0,5; h = 0,75 a po změně k na 0,75.
• Postupuj analogicky jako v předchozím příkladě, tj. odvozuj L pro první k, a to pro první důchod 100, resp. druhý důchod 200. Pak totéž pro druhé k, celkem 4 přímky L. Jsou přímky L rovnoběžné a proč? Čím se liší první dvojice L od druhé? Jaký to má grafický důsledek pro LM?
• Zapiš změny a jejich důsledky symbolicky (jako pravidlo k zapamatování) pomocí implikací.

Změna h

• Analyzuj početně i graficky pro k = 0,5; h = 0,75 a po změně h na 0,8.
• Postupuj analogicky jako v předchozím příkladě, tj. odvozuj L pro první h, a to pro první důchod 100, resp. druhý důchod 200. Pak totéž pro druhé h , celkem 4 přímky L. Jsou přímky L rovnoběžné a proč? Čím se liší první dvojice L od druhé? Jaký to má grafický důsledek pro LM?
• Zapiš změny a jejich důsledky symbolicky (jako pravidlo k zapamatování) pomocí implikací.

Změna sklonu IS vliven snížení citlivosti investic na úrokovou míru

• Analyzuj početně i graficky pro AD = 1 000 + 0,7.Y - b.i, kde výchozí b = 40 a nové b = 5 (odvozujte vždy pro úrokové míry 10, resp. 5).
• Odvozuj rovnice AD pro první b, a to pro jednu, resp. druhou úrokovou míru. Pak totéž pro novou b, celkem tedy 4 přímky AD. Jsou přímky AD rovnoběžné a proč? Čím se liší první dvojice AD od druhé? Jaký to má grafický důsledek pro IS?
• Zapiš změny a jejich důsledky symbolicky (jako pravidlo k zapamatování) pomocí implikací.

Změna sklonu IS vlivem změny alfa

• Modeluj zvýšení daňové sazby analyticky a výsledek zakresli. Zapiš výsledek symbolicky.

• Modeluj zvýšení daňové sazby graficky a srovnej s předchozím výsledkem.

• Např. zvol autonomní výdaje 1 000; citlivost inveMstic na úrokovou míru 40; mezní sklon ke spotřebě 0,8; výchozí daňovou sazbu 0,20; novou daňovou sazbu 0,25.

• První dva body zopakuj pro změnu mezního sklonu ke spotřebě (pro t = 0,20).

Sklon a posun IS

• Co určuje sklon IS a vyvolává změnu sklonu IS? Odvoď a zapiš symbolicky.
• Co určuje posun IS a vyvolává změnu posunu IS? Odvoď a zapiš symbolicky.

Sklon a posun LM

• Co určuje sklon LM a vyvolává změnu sklonu LM? Odvoď a zapiš symbolicky.
• Co určuje posun LMa vyvolává změnu posunu LM? Odvoď a zapiš symbolicky.

Křivky IS, LM

• Urči závislosti IS, LM.
• Odvoď rovnováhu na trhu zboží početně, resp. graficky.
• Odvoď rovnováhu na trhu peněz početně, resp. graficky.

Změna kvality vládních výdajů

·   V ekonomice dojde ke snížení transferových plateb a současně ke zvýšení vládních nákupů zboží a služeb o stejný objem.

·      Odvoďte teoreticky, jaký vliv má přesun na úroveň rovnovážného důchodu (modelujte rovnováhu před, resp. po změně; odečtěte). 

·     Své úvahy ověřte výpočtem pro mpc = 0,8; t = 0,2; přesun vládních výdajů z položky transfery na vládní nákupy zboží a služeb je 50 jednotek. Jaká je změna rovnovážného důchodu.

·     Na základě získaných znalostí popište současné intervence vlády a jejich důsledky (citujte z tisku a komentujte).