Makroekonomická rovnováha v čase

Příklad ze cvičení

Makroekonomická rovnováha v čase

Určete, jak se vyvíjí důchod v čase, je-li mpc = 0,6; autonomní C = 160; autonomní I = 40. Zpoždění mezi důchodem a poptávkou je o jedno období.

• Jaká je statická rovnováha? Také obecně.
• Zapiš rovnici zpožděné AD v jednosektorové ekonomice.
• ... ve dvousektorové.
• Jaký je vývoj důchodu v dlouhém období (řeš diferenční rovnici)?
• Urči vývoj důchodu pro počáteční podmínku důchod v čase nula = 600. 
• Situaci zakresli.
• Zapiš obecně, kam se blíží důchod v dlouhém období (limitou.)

Dynamický model S-D, zpoždění na straně poptávky

• Přehoď v modelu S-D (viz předchozí příklady) zpoždění na stranu poptávky, a to pro oba předchozí poměry sklonů S, resp. D.
• Řeš nejprve matematicky a pak teprve graficky. Zkontroluj pokaždé souhlas.
• Zapiš přehledně a systematicky všechny čtyři případy dynamické rovnováhy S-D pro nespojité změny.

Nekonvergentní nespojitý model S-D při zpoždění na straně nabídky

• Přehoď vzájemný poměr sklonů z předchozích příkladů.
• Vykonej všechny kroky z předchozích příkladů.
• Přehledně zapiš srovnání.

Početní určení konvergence v pavučinovém modelu S-D

• Mějme S: Q = - 1 + 2 P; D: Q = 24 - 3 P; počáteční cena je rovna 3 jednotkám. Zpoždění je o jedno období straně nabídky.
• Zapiš rovnice dynamické rovnováhy, tj. diferenční rovnici.
• Řeš rovnici ve všech bodech s matematickým popisem.
• Spočti také partikulární řešení odpovídající počáteční podmínce.
• Vypiš předpis (funkci), která charakterizuje vývoj cen v čase.
• Interpretuj řešení, tj. vytvoř tabulku hodnot nalezené funkce vývoje cen v čase.
• Zakresli vývoj cen v čase, resp. vývoj odchylek v čase (z hodnot v tabulce).
• Zkontroluj správnost porovnáním s grafickým řešením, resp. s intuitivním odhadem.
• Změň počáteční podmínku na počáteční cenu rovnu 2 jednotkám. Zakresli, popiš.
• Interpretuj, co znamená změna počáteční podmínky (dle grafu). 

Grafické určení a znázornění konvergence v pavučinovém modelu S-D

• Mějme S: Q = - 1 + 2 P; D: Q = 24 - 3 P; počáteční cena je rovna 3 jednotkám. Zpoždění je o jedno období na straně nabídky.
• Zakresli S, D do přehledného grafu přesně v měřítku.
• Vyznač vývoj tlaků na změny ceny v čase, tj. zakresli "pavučinu" ke grafu S-D.
• Vyznač velikost odchylek od rovnovážné ceny na straně nabídky. Označ p0, p1, p2 atd.
• Zakresli graf vývoje odchylek, resp. absolutních hodnot odchylek v čase.
• Zakresli vývoj cen v čase.
• Zapiš limitu týkající se vývoje odchylek v čase a odpovídající konvergenci, resp. divergenci modelu.

Intuitivní odhad konvergence v pavučinovém modelu S-D

• Mějme S: Q = - 1 + 2 P; D: Q = 24 - 3 P; počáteční cena je rovna 3 jednotkám. Zpoždění je o jedno období na straně nabídky.
• Odhadněte intuitivně (pomocí porovnání sklonů S, D), zda je model konvergentní, tj. zda situace spěje k rovnovážné ceně.
• Jedná se o model nespojitý nebo spojitý?

Extrémní účinky fiskální, resp. monetární politiky

• Systemizuj všechny případy extrémní účinnosti fiskální, resp. monetární politiky. 
• Vždy zakresli obrázek, popiš účinnost na základě grafického vyjádření.
• Pro každý případ spočti účinnost na základě limity multiplikátoru.

Změna důchodu vlivem změny nabídky peněz

• Pro výše zadanou ekonomiku zvol změnu nabídky peněz.
• Počítej dvěma metodami (multiplikátory, resp. průsečíky přímek)
• Řeš graficky (přesný nákres se změřením délek úseček).
• Výsledky porovnej. V případě neshody oprav.

Velikost vytěsněné produkce vlivem změny daňové sazby

Urči velikost vytěsněné produkce vlivem snížení daňové sazby z hodnoty 0,25 na hodnotu 0,20.

• Ekonomika je popsána stejně jako v předchozím příkladě.
• Lze počítat oběma metodami jako v předchozím příkladě?
• Řeš také graficky (přesné zakreslení a ověření hodnot z grafu).
• Zapiš výsledky početního i grafického výpočtu symbolicky s využitím implikací (jako pravidlo). Došlo k posunu nebo otočení přímek v modelu IS-LM, a které.

Velikost vytěsněné produkce vlivem změny  vládních výdajů

Urči velikost vytěsněného produktu vlivem fiskální politiky vlády v podobě zvýšení vládních výdajů o 100 jednotek. 

• Počítej pro autonomní spotřebu 100, mpc = 0,8; pro t = 0,25; transfery jsou ve výši 125 a vládní výdaje 400. L = 0,5.Y - 50.i; I = 300 - 30.i; nabídka peněz vztažená k cenové hladině je 500.
• Počítej dvěma metodami, a to (a) srovnáním multiplikátorů a (b) určením průsečíků přímek a jejich souřadnic důchodu. 
• Řeš také graficky (přesné zakreslení a ověření hodnot z grafu).
• Zapiš výsledky početního i grafického výpočtu symbolicky s využitím implikací (jako pravidlo). Došlo k posunu nebo otočení přímek v modelu IS-LM, a které.

Změna sklonu LM vlivem změny k, resp. h

  Změna k

• Analyzuj početně i graficky pro k = 0,5; h = 0,75 a po změně k na 0,75.
• Postupuj analogicky jako v předchozím příkladě, tj. odvozuj L pro první k, a to pro první důchod 100, resp. druhý důchod 200. Pak totéž pro druhé k, celkem 4 přímky L. Jsou přímky L rovnoběžné a proč? Čím se liší první dvojice L od druhé? Jaký to má grafický důsledek pro LM?
• Zapiš změny a jejich důsledky symbolicky (jako pravidlo k zapamatování) pomocí implikací.

Změna h

• Analyzuj početně i graficky pro k = 0,5; h = 0,75 a po změně h na 0,8.
• Postupuj analogicky jako v předchozím příkladě, tj. odvozuj L pro první h, a to pro první důchod 100, resp. druhý důchod 200. Pak totéž pro druhé h , celkem 4 přímky L. Jsou přímky L rovnoběžné a proč? Čím se liší první dvojice L od druhé? Jaký to má grafický důsledek pro LM?
• Zapiš změny a jejich důsledky symbolicky (jako pravidlo k zapamatování) pomocí implikací.

Změna sklonu IS vliven snížení citlivosti investic na úrokovou míru

• Analyzuj početně i graficky pro AD = 1 000 + 0,7.Y - b.i, kde výchozí b = 40 a nové b = 5 (odvozujte vždy pro úrokové míry 10, resp. 5).
• Odvozuj rovnice AD pro první b, a to pro jednu, resp. druhou úrokovou míru. Pak totéž pro novou b, celkem tedy 4 přímky AD. Jsou přímky AD rovnoběžné a proč? Čím se liší první dvojice AD od druhé? Jaký to má grafický důsledek pro IS?
• Zapiš změny a jejich důsledky symbolicky (jako pravidlo k zapamatování) pomocí implikací.

Změna sklonu IS vlivem změny alfa

• Modeluj zvýšení daňové sazby analyticky a výsledek zakresli. Zapiš výsledek symbolicky.

• Modeluj zvýšení daňové sazby graficky a srovnej s předchozím výsledkem.

• Např. zvol autonomní výdaje 1 000; citlivost inveMstic na úrokovou míru 40; mezní sklon ke spotřebě 0,8; výchozí daňovou sazbu 0,20; novou daňovou sazbu 0,25.

• První dva body zopakuj pro změnu mezního sklonu ke spotřebě (pro t = 0,20).

Sklon a posun IS

• Co určuje sklon IS a vyvolává změnu sklonu IS? Odvoď a zapiš symbolicky.
• Co určuje posun IS a vyvolává změnu posunu IS? Odvoď a zapiš symbolicky.

Sklon a posun LM

• Co určuje sklon LM a vyvolává změnu sklonu LM? Odvoď a zapiš symbolicky.
• Co určuje posun LMa vyvolává změnu posunu LM? Odvoď a zapiš symbolicky.

Křivky IS, LM

• Urči závislosti IS, LM.
• Odvoď rovnováhu na trhu zboží početně, resp. graficky.
• Odvoď rovnováhu na trhu peněz početně, resp. graficky.

Změna kvality vládních výdajů

·   V ekonomice dojde ke snížení transferových plateb a současně ke zvýšení vládních nákupů zboží a služeb o stejný objem.

·      Odvoďte teoreticky, jaký vliv má přesun na úroveň rovnovážného důchodu (modelujte rovnováhu před, resp. po změně; odečtěte). 

·     Své úvahy ověřte výpočtem pro mpc = 0,8; t = 0,2; přesun vládních výdajů z položky transfery na vládní nákupy zboží a služeb je 50 jednotek. Jaká je změna rovnovážného důchodu.

·     Na základě získaných znalostí popište současné intervence vlády a jejich důsledky (citujte z tisku a komentujte).

Spotřeba ve třísektorové ekonomice

• Je dána spotřební funkce C = 200 + 0,8 YD (disponibilní důchod).
• Investice jsou ve výši 100, vládní výdaje jsou 300, transferové platby 125, autonomní daně 100 a daňová sazba 0,25.
• Jaká je velikost multiplikátoru?
• Jaká je velikost celkové spotřeby?

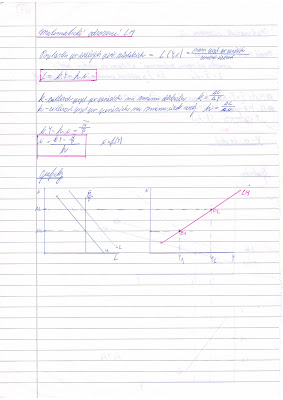
 Dvousektorová ekonomika

• Předpokládejme, že GNP = 1000 jednotek, přičemž C = 800 a I = 200, mpc = 0,5.
• Firma se rozhodne postavit sklad a její investice se zvýší z 200 na 210 jednotek.
• Popište přechod od staré rovnováhy k nové.
• Určete velikost přírůstku důchodu (odečtením dvou předchozích rovnic).
• Popište multiplikační účinek, tj. o kolik se zvýší GNP, když investice se zvýší o 10 jednotek.
• Zakreslete starou a novou rovnováhu, vyznačte změny I a GNP.
• Popište v obrázku multiplikační efekt.

Pokles daňové sazby

• Ekonomika je dána těmito parametry: Důchod je 1000, mpc = 0,8, sazba důchodové daně se změní z 0,3 na 0,2.
• Popište rovnicemi AD před změnou a po změně.
• Danou změny AD zakreslete. Zobrazte změnu rovnovážné úrovně důchodu.
• Změnu důchodu kvantifikujte.
• O kolik se změní daňové příjmy vlády?

Maximalizace užitku

Akumulace kapitálu

Paradox velké úrody, resp. snížení poplatků za telefon

Elasticita funkce

Cenová elasticita poptávky vyjadřuje reakci spotřebitele na relativní změnu ceny zboží, která se projeví relativní změnou jeho poptávaného množství.

Elasticita funkce v bodě je relativní míra (rychlost) stejných změn. Slovo relativní je chápáno jako rychlost ve vztahu k celku.

Funkce je:

• elastická,  je-li |ED| >1
• neelastická, je-li |ED| < 1
• jednotkově elastická, je-li |ED| = 1

Elasticitu funkce lze zjistit jako poměr mezních veličin a průměrných veličin funkce. 

|ED| = |Mf|/|Af|

Grafické určení elasticity:

Pro grafické určení elasticity funkce v bodě je nutné sestrojit tečnu křivky v daném bodě a spojnici daného bodu s počátkem.

Je-li a_A  < a_{M, pak je funkce v bodě X elastická.}

Je-li a_A > a_{M, pak je funkce v bodě X neelastická.}

Hledání extrémů funkce

Postup při zjišťování extrémů funkce:

1. Zjistíme první derivaci dané funkce.
2. První derivaci funkce položíme nule a zjistíme kořeny vzniklé rovnice. Kořeny zmíněné rovnice mohou, ale také nemusí být lokální extrémy funkce.  Tyto body se nazývají body podezřelé z extrému, neboli stacionární body.
3. Zjistíme druhou derivaci funkce.
4. Do druhé derivace dosadíme stacionární bod.
5. Rozhodneme o povaze extrému podle znaménka druhé derivace:

• f´´ > 0       jedná se o lokální MINIMUM
• f´´ < 0       jedná se o lokální MAXIMUM
• f´´ = 0       jedná se o INFLEXNÍ BOD

Inflexní bodem se názývá bod, ve kterém funkce přechází z konvexní do konkávní a naopak.

Příklad:

Hledání bodu zvratu funkce

• Urči bod zvratu funkce TC: C(Q) = Q^3 - 12 Q^2 + 60 Q.
• Urči funkce MC a AC, zakresli do navazujícího grafu.
• Vyznač tečnu ke grafu funkce TC v bodě zvratu a popiš její chování.
• Sleduj vztah funkcí MC a AC, a to v bodě zvratu a kolem něj.

Maximalizace zisku

Urči maximum zisku, je-li: TR = 1 400 Q - 7,5 Q^2; TC = Q^3 - 6 Q^2 + 140 Q + 750. Počítej pomocí ekonomického pravidla, resp. matematickým postupem.

Nakresli pod sebe 3 související grafy: 1. TR a TC, 2. zisk, 3. MR a MC. 

Vyznač tečny ke grafům funkce TR a TC v bodě zvratu.

Úkoly z 3. cvičení

Progresivní a degresivní změny

Hladká funkce

Funkce je hladká v případě, že má spojitou derivaci.

"Klikatka"